수학다락방의 참여방법을 한번 바꿔 보았습니다.(참여방법 설명은 프리뷰영상에도 있어요 :) )
이번달에는 키워드(#소수#집합#부등식)중 2개 이상의 키워드가 포함된 수학 문제를 직접 만들어보세요!!
문제를 만들기 위해서는 키워드의 개념을 정확히 알아야 하고, 개념-개념을 연결하는 것들이 어떤것이 있을지 많은 고민을 해야 할것 같아요!!
그래도 여러분의 창의적인 생각과 친구들과의 토론이 이어진다면, 정말 멋진 문제가 만들어 지지 않을까 생각합니다.
친구들의 문제에 오류가 있는지, 친구들의 문제 해결방법을 안다면 댓글을 남겨주세요 :)
아래 예시를 확인하고, 여러분도 친구들과 풀어볼 문제를 꼭 만들어보세요!!
주제 프리뷰영상 : 변경된 참여방법 꼭 확인하세요!!
이번달에는 키워드(#소수#집합#부등식)중 2개 이상의 키워드가 포함된 수학 문제를 직접 만들어보세요!!
문제를 만들기 위해서는 키워드의 개념을 정확히 알아야 하고, 개념-개념을 연결하는 것들이 어떤것이 있을지 많은 고민을 해야 할것 같아요!!
그래도 여러분의 창의적인 생각과 친구들과의 토론이 이어진다면, 정말 멋진 문제가 만들어 지지 않을까 생각합니다.
친구들의 문제에 오류가 있는지, 친구들의 문제 해결방법을 안다면 댓글을 남겨주세요 :)
아래 예시를 확인하고, 여러분도 친구들과 풀어볼 문제를 꼭 만들어보세요!!

주제 프리뷰영상 : 변경된 참여방법 꼭 확인하세요!!



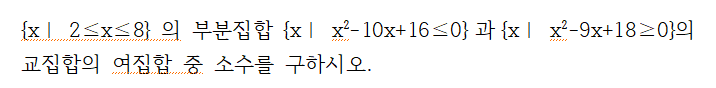
본인이 생각하는 질문
20면의 회원들이 비행기의 의자에 앉으려고 하는데 , 한 줄에는 10명이하의 소수명의 살람들이 앉을 수 있다.
이때, 회원들이 각 줄에 앉을 수 있는 방법의 경우를 집합으로 표현해보면?
예를 들어, 각 줄에 5명씩 앉는 다면 {5,5,5,5}라고 표현한다.
(단, 순서 바꾸는 것은 하나로 친다.)