
6월 수학 다락방 키워드는 #원#다각형#넓이 입니다.
키워드가 포함된 수학 문제를 올려주세요. 친구들이 올린 문제를 풀면서 여러분의 수학 지식을 넓혀 보세요 :)
6월 주제 프리뷰 영상









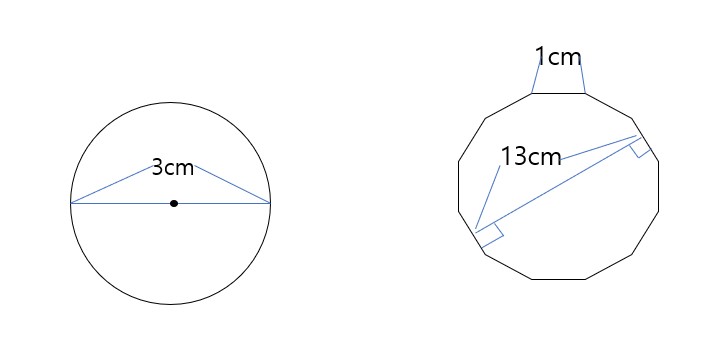 다음 원의 둘레와 정12각형의 넓이의 곱을 구하시오.(원주율:3.141)
다음 원의 둘레와 정12각형의 넓이의 곱을 구하시오.(원주율:3.141)






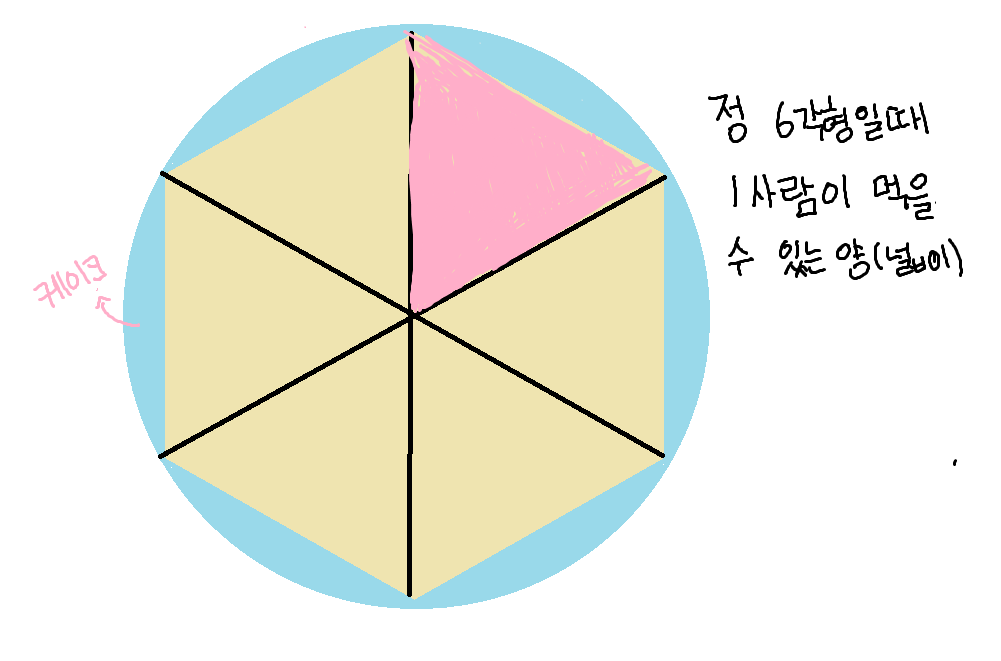
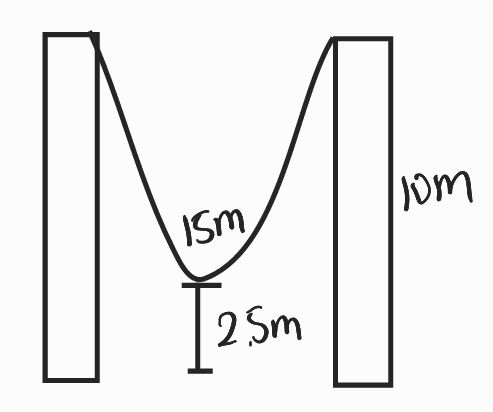
정육각형 모양의 벽시계의 시계바늘이 9시를 가리키고 있다. 시계바늘들이 만드는 작은쪽의 각이 만드는 다각형의 넓이를 구해라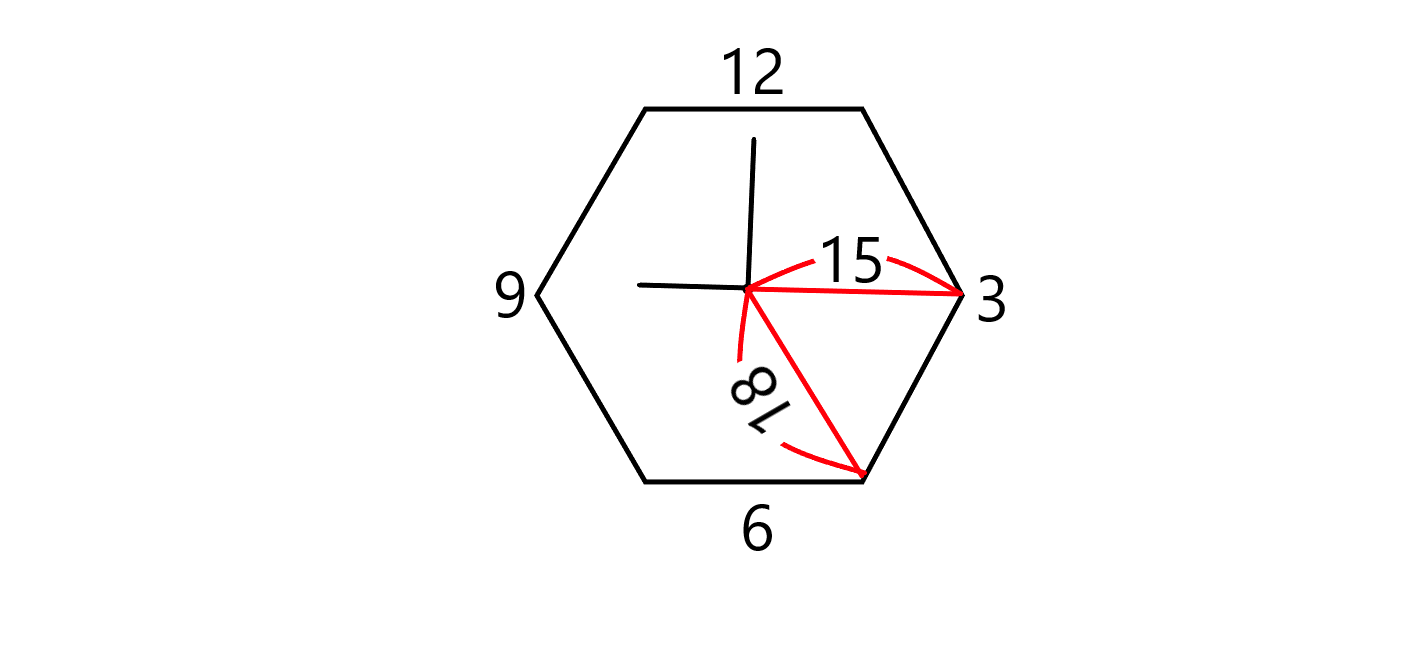





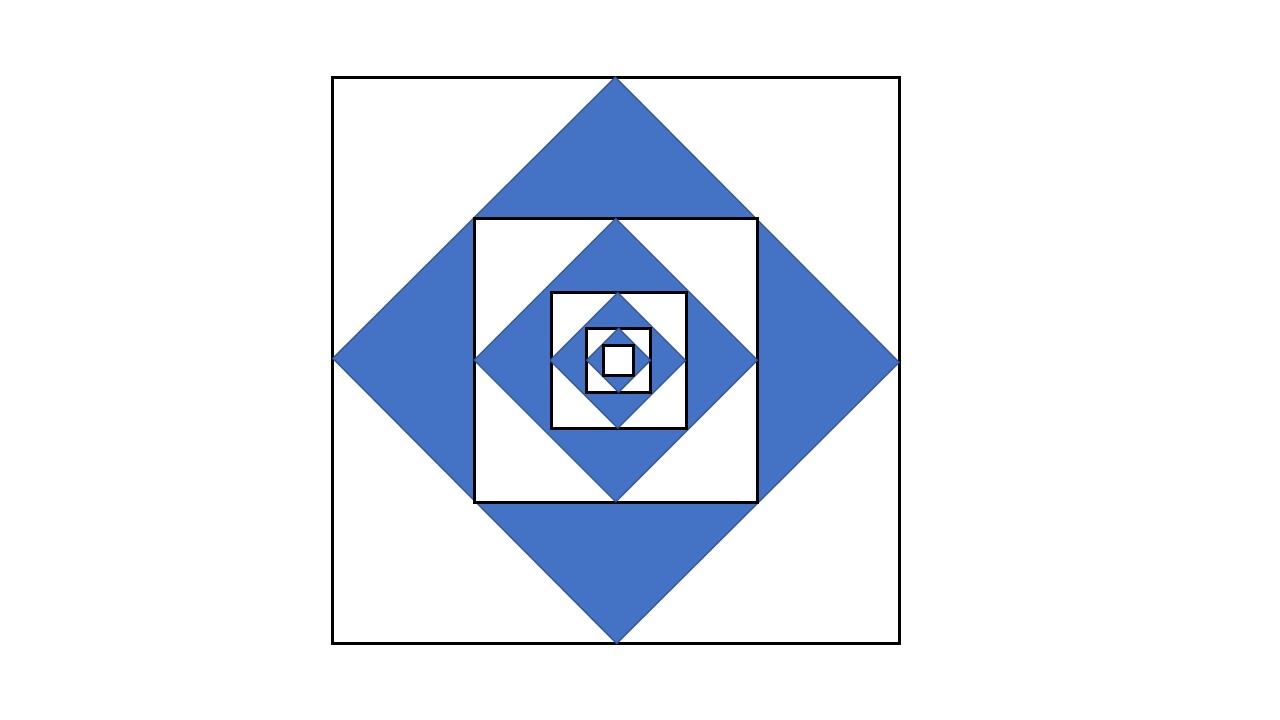
 <- 예시(정 6각형일 때)
<- 예시(정 6각형일 때)

구면은 2차원에는 원, 3차원에는 구, 그리고 4차원에는 초구로 표현됩니다.
초구는 xyz축 이외 w축이 더해지면서 만들어지는 4차원 공간 속의 도형으로, 단면을 잘랐을 때 잘린 부분이 구의 모습을 띄고 있습니다.
3차원의 우리는 하위차원인 0,1,2차원의 도형을 볼 수 있지만, 상위차원인 4,5,6…N차원의 도형은 볼 수 없습니다.
그렇다면 시각적으로 보여지지 않는 도형의 면적은 어떻게 구할 수 있을까요?
2차원 원의 넓이나 3차원 구의 부피를 활용하여 구하는 방법은 없을까요?
좋아하는 SF 영화에서 5차원의 공간을 표현한 장면이 있었습니다.
그후, 고차원의 공간과 그 공간에 있는 물체의 모습은 어떠할지 상상해보게 되었고, 3차원의 인간이 고차원 도형의 면적을 알아낼 수 있는 방법을 찾는다면, 고차원에 대한 이해가 높아질 것 같다는 생각이 들었습니다.
















 ㅍ
ㅍ














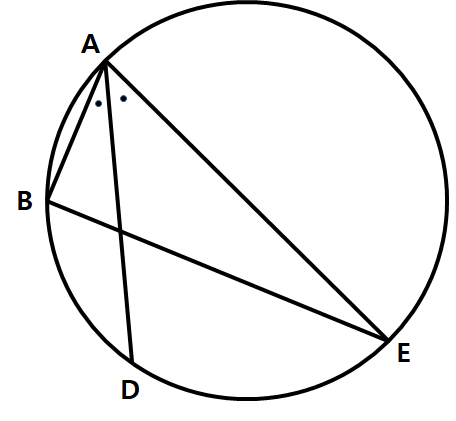
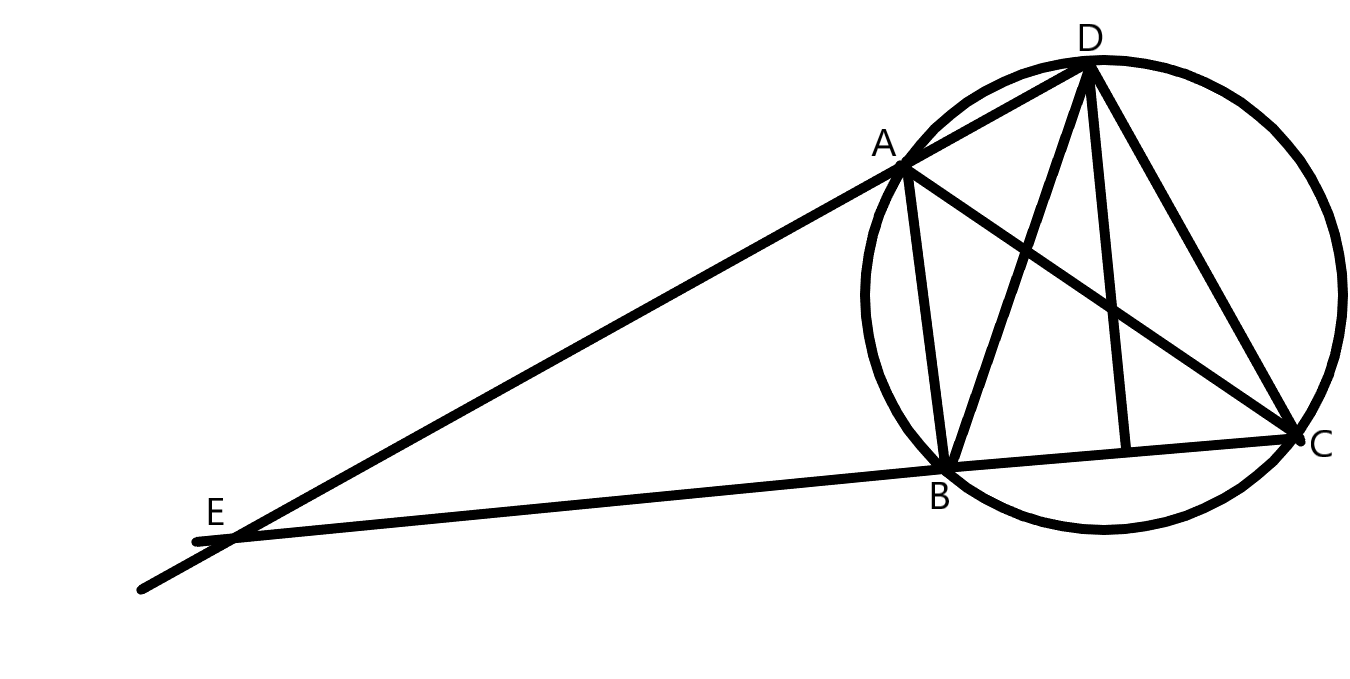
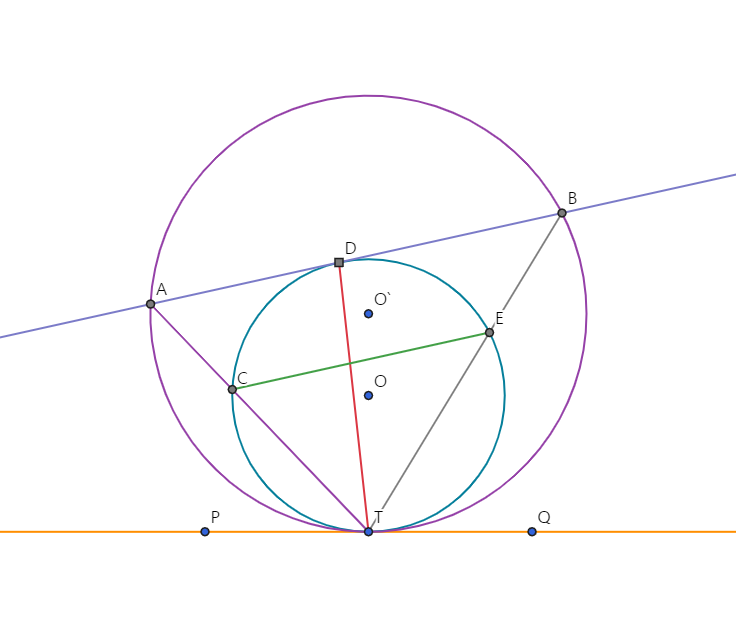
 \(\overline{AC}\)의 교점은 F, 직선 AI와 \(\overline{B
C}\)의 교점은 E,
\(\overline{AC}\)의 교점은 F, 직선 AI와 \(\overline{B
C}\)의 교점은 E,  직선 CI와 \(\overline{AB
}\)의 교점은 D다. 여기서, \({\overline{AI} \over \overline{IE}}={p \over q} (gcd(p,q)=1)\) 다.
직선 CI와 \(\overline{AB
}\)의 교점은 D다. 여기서, \({\overline{AI} \over \overline{IE}}={p \over q} (gcd(p,q)=1)\) 다.
































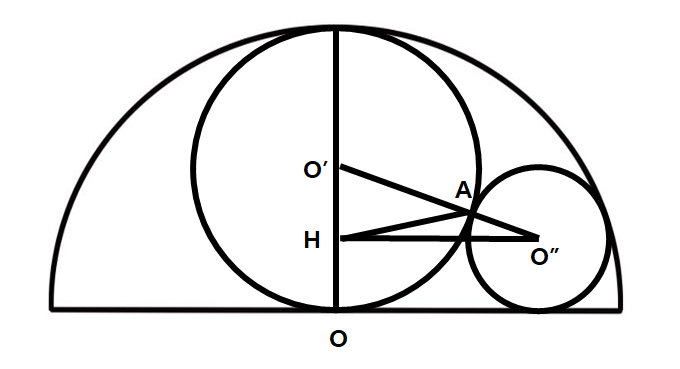
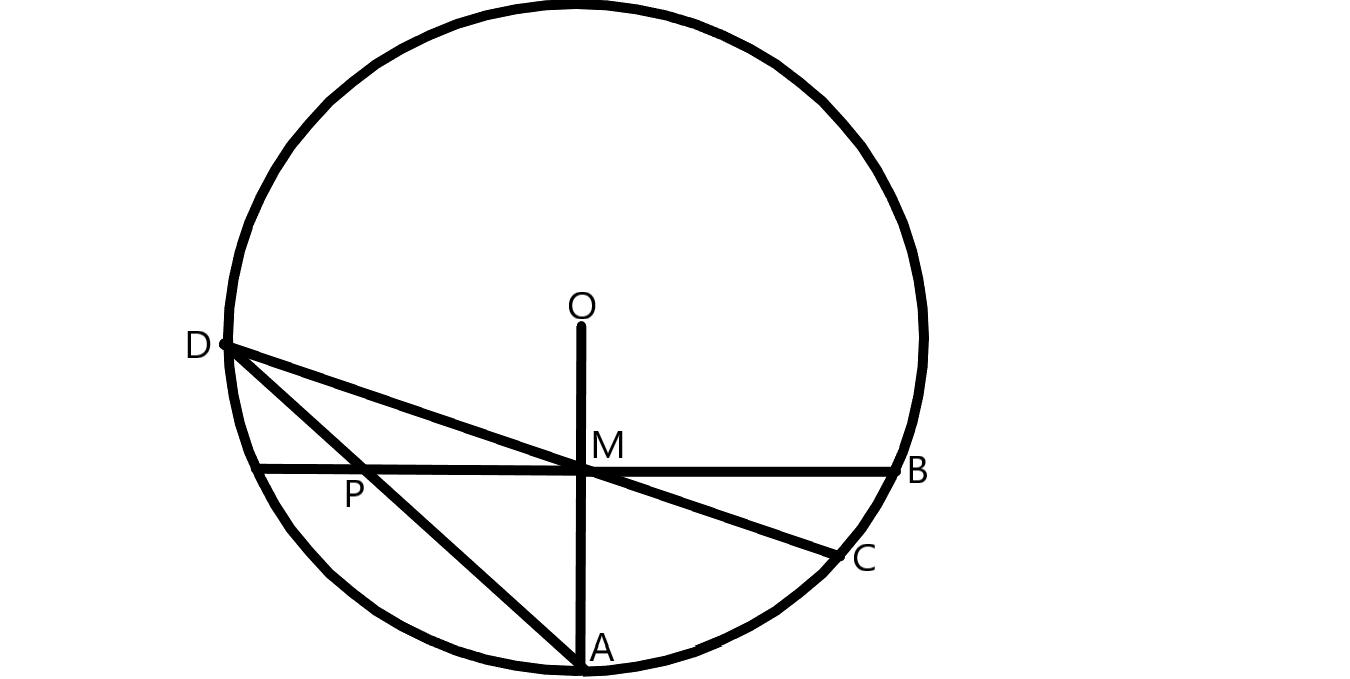 반지름이 12인 원 O 위의 한 점 A에 대하여 선분 OA의 중점 M을 지나고 OA에 수직인 직선 l이 원 O와 만나는 점 중 하나를 B라 하자. 점 C는 호 AB위의 점으로 직선 CM이 원 O와 만나는 점 D(D≠C)에 대하여 CD=21이다. 직선 AD와 직선 l이 만나는 점을 P라 할때 CP^2를 구하여라.
반지름이 12인 원 O 위의 한 점 A에 대하여 선분 OA의 중점 M을 지나고 OA에 수직인 직선 l이 원 O와 만나는 점 중 하나를 B라 하자. 점 C는 호 AB위의 점으로 직선 CM이 원 O와 만나는 점 D(D≠C)에 대하여 CD=21이다. 직선 AD와 직선 l이 만나는 점을 P라 할때 CP^2를 구하여라.











학원에서 보던 문제를 풀다가 점화식을 조건을 빼놓고 세웠다는 사실을 알게 되었습니다. 그 점화식을 활용해 보고자 그 조건을 빼놓은 문제를 만들어 보았습니다. 이 문제를 보자마자 2^n-nC0-nC1-nC2를 생각하는 사람이 있겠지만 다른 방법으로 풀기를 바랍니다. 저는 점화식을 이용해 해결하였습니다.









본인이 생각하는 질문
한 변의 길이가 1인 정육각형 큐브가 있을 때, 이 큐브를 여러 방향으로 돌렸을 때 이 큐브의 그림자의 넓이의 평균은 얼마일까?
다만, 광원은 큐브로부터 무한히 떨어져 있다.
여기서 평균은 큐브의 모든 그림자의 넓이의 평균이다.