삼각형에서 페르마 포인트란 삼각형 안의 무수히 많은 점 중에서 세 꼭짓점까지의 각각 거리의 합이 최소가 되는 점을 뜻한다. 사각형에서도 물론 페르마 포인트가 있지만 2개가 나온다. 사각형의 네 꼭짓점까지의 거리의 합이 최소가 되는 오로지 하나의 점이 있을 것인데, 어떻게 구할 수 있을까? 또한 페르마 포인트를 다른 곳에, 예를 들면 입체도형에, 적용할 수 있을까?

이번 주제의 내용이 최단 거리와 관련된 것을 보고 예전에 경시대회 준비를 하면서 배웠던 페르마 포인트에 관한 내용이 생각났다. 그래서 관련된 내용을 찾아보다가 이런 궁금증이 생기게 되었다.

Fermat_points.png

우리가 최단거리는 그 지점 까지의 직선 거리밖에 없을까?

보통 최단거리라 하면 직선거리를 생각하는데 오직 최단거리를 직선거리로만 생각할 수 있는지 궁금했다.

울퉁불퉁한 사이클로이드 곡선과 기울어진 울퉁불퉁한 직선에 공을 굴리면 어느 것이 더 빠르게 바닥에 도착할수 있을까? 

마찰력 때문에 속도가 느려져서 같은 시간에 내려오는지, 다른 시간에 내려오는지 궁금하다.

비행기 동선을 짤때 일반적으로 최단거리를 정하는것이 아닌 지구의 곡률을 고려해 보다 정밀하게 거리를 정한다. 구면에서의 최단거리를 가장 쉽게 구할 수 있는 방법에는 뭐가 있을까?

비행기에서 목적지로 도달하는 경로를 정하는 과정을 보다 근사하여 쉽게 구할 수 있는 방법을 없을까 하는 의문이 들어서

좌표평면 위에 원이 있다. 원의 반지름은 8이다. 원 위의 두 점과 맞닿도록 곡선을 위치한다. 이 곡선 위에서 이동하는 한 점이 있다고 할 때, 이 점이 원의 중심을 거쳐 원과 곡선이 닿는 두 지점 중 한 지점에 도착할 최단경로는 어떻게 될까? 직선을 활용하여 측정할 수 있을까?

좌표평면 위에 원과 곡선이 놓여있을 때, 직선을 이용하여 경로를 측정할 수 있을지 의문이 생겼다.

실생활에서 직선 최단거리를 찾는 것이 의미가 있을까?

세상은 완벽한 평면이 아닌 둥근 형태를 하고 있어 거리를 잴 때도 사실 직선이 아닌 곡선의 형태를 보게 된다. 이때문에 거리 계산을 할 때도 미세하지만 오차가 생길텐데, 차라리 처음부터 컴퓨터 등을 통해 약간의 곡선을 고려하여 계산하는 것이 더 정확할 것 같다 생각하게 되었다.

우주에서 비행체가 효율적으로 이동하기위해선 최단거리가 필요할것이다. 내가 생각하기엔 우주에서 최단거리는 점(출발지)과 점(도착지)사이를 연결해주는 선분의 길이일것이다.  하지만 그 사이를 가로막는 우주먼지같은 장애물이나 중력의 영향을 받는다면 이동경로는 바뀔것이다. 대규모 우주 비행시 비행체의 이동경로를 다루는 직원은 어떤 경로를 만들었고 무슨 이유로 그렇게 만들었는지 궁금하다. 예를들면 보이저 2,1호 가 있을것같다.

최단 경로(주제)에 대해 고민하다가 갑자기 든 생각이다. 지구도 평면이라 볼수있지만 멀리서 보면 구와 비슷한 모양을 갇춘다. 하지만 사방이 뚫려있고 어디든지 갈수 있는 우주에선 다를것같았다. 우주도 지구와 같이 가까운거리는 단순하게 직선 모양을 띨지 몰라도 그 거리가 멀어진다면 지구에선 곡선형태의 최단경로가 나오듯 우주에서도 다른 모양의 경로가 나올것이라는 생각이 들었다. 

1. 사이클로이드가 낙하 상황에서 직선거리보다 더 짧음을 어떻게 증명할까?
2. 사이클로이드보다 짧은 거리가 없음을 어떻게 증명할까? ( 사이클로이드보다 더 짧은 거리는 없을까?)
3. 이런 사이클로이드를 실생활에서 활용하는 예시는 어떤 것이 있을까? ( 사이클로이드를 실생활에서 어디에 활용할 수 있을까?)

먼저 평소엔 직선거리가 최단거리라고 생각했는데 사이클로이드라는 최단거리가 있다는 것이 놀라웠고,
육안으로 보기엔 직선거리가 더 짧아 보이는데 왜 사이클로이드가 더 짧은지 궁금했다.
만약 사이클로이드가 낙하상황에서 최단거리라면, 이것을 실생활에서 어떻게 활용할 수 있을지 궁금하다

이상적이지 않은 도형(현실세계의 도형)의 둘레를 어떻게 구할까?

미적분을 공부하면 길이에 대한 정적분에 대해 알게된다.
하지만 여기서 나오는 함수는 이상적인 , 즉 수학책에서만 나오는 함수이다. 그렇다면 실제 세상에 있는 우리가 함수로 만들 수 없는 것(좌표평면에 그 도형을 올려놓다고 해서 자취의 방정식을 구할 수 없다고 생각함)의 길이는 어떻게 구할수 있을까?

사이클로이드 곡선 형태인 롤러코스터는 직선 형태인 롤러코스터보다 더 빨리 떨어진다.
그렇다면, 사이클로이드보다 더 굴곡이 진 형태의 롤러코스터는
사이클로이드 형태나 직선 형태의 롤러코스터보다는 더 빨리 떨어질까?
그 이유는 무엇일까?
 

최근 현장학습 체험에서 롤러코스터를 타면서 궁금해졌다.

위 이차함수 그래프에서 A에서부터 x 값이 -2인 지점까지의 최단거리는 어떻게 측정할 수 있을까? 곡선을 직선으로 변형하는 과정은 어떻게 사용할 수 있을까? 포물선에서의 최단거리 등을 구하려면 어떤 과정을 거쳐야하는 것일까?

프로그램을 이용해 이차함수 포물선을 그려보았다. 곡선에서의 거리 측정과 직선으로 변환하려면 어떤 과정을 거쳐야할지가 궁금하였다.

1. 사이클로이드는 물체가 하강할 때의 최단 경로이다. 하지만 실생활에서는 사이클로이드를 찾아보기 쉽지 않다. 그 이유는 무엇일까?
2. 만약 사이클로이드가 사용되는 곳이 있다면 어디에 사용될까?

사이클로이드는 물체가 하강할 때의 최단 경로이므로 효율적일텐데 생활속에서 사이클로이드를 본 경험이 별로 없기 때문에 그 이유가 궁금했고, 사이클로이드가 사용되는 곳을 알고 싶었다.

왜 사이클로이드 곡선을 따라갔을 때 시간이 제일 적게 걸릴까?(직선이 아니라)

정확한 증명이 궁금했다.

우리가 사는 세계에서는 두 점 사이에서의 최단거리가 존재한다.

이 최단거리는 모든 상황에서 존재할까?

갑자기 생각났다.

지구처럼 표면이 휘어진 모양인 공간에서는 최단 거리를 구하려 두 지점를 잇는 선분을 그리면
표면을 뚫고 들어가게 되기 때문에 현실적으로는 두 지점 사이에 이동이 불가능한 경로가 된다. 그렇다면 구 위 두 점을
잇는 최단 경로는 어떻게 구할 수 있을까?

세계 지도에서 두 지점을 잇는 최단 거리 항로를 구할 때 직선으로 이은 것보다 곡선으로 약간 휘게 그리는 것이
더 옳다고 한다. 그래서 이 질문을 하게 되었다.

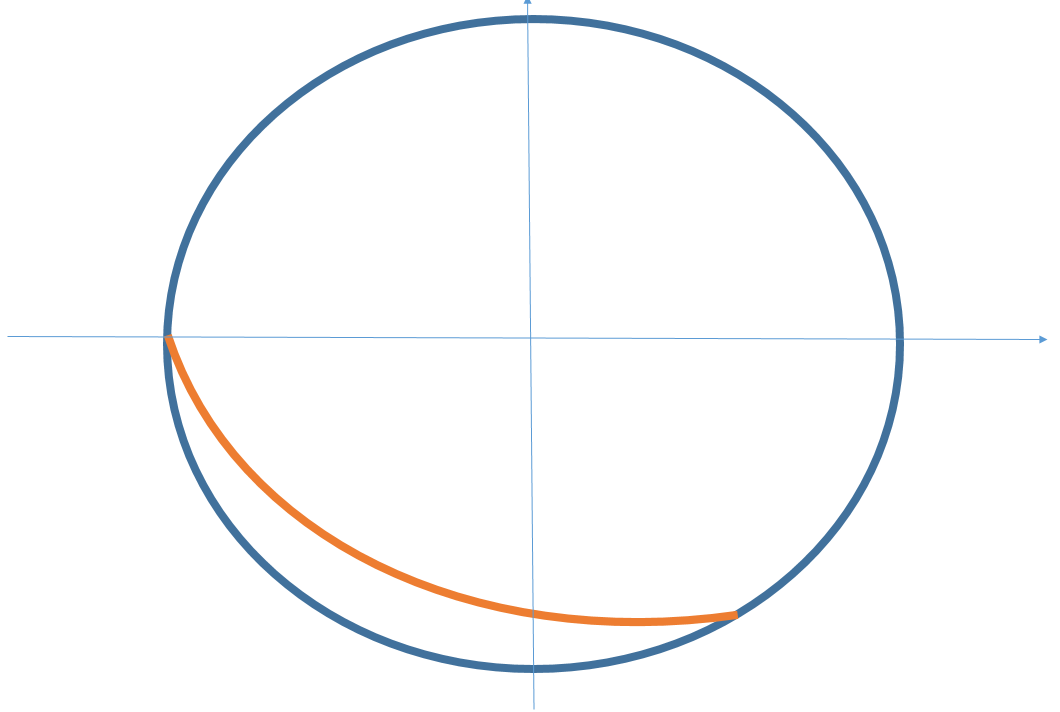
두 개의 거울이 60°를 이루고 있다.

한 점에서 거울을 향해 빛을 쏘았을 때,  입사 광선과 반사 광선으로 별 모양이 나올 수 있을까? 별 모양이 나온다면, 빛의 입사각은 몇 도일까?

(이때, 별 모양을 이루는 선분의 길이와 각도의 크기는 같지 않아도 된다.)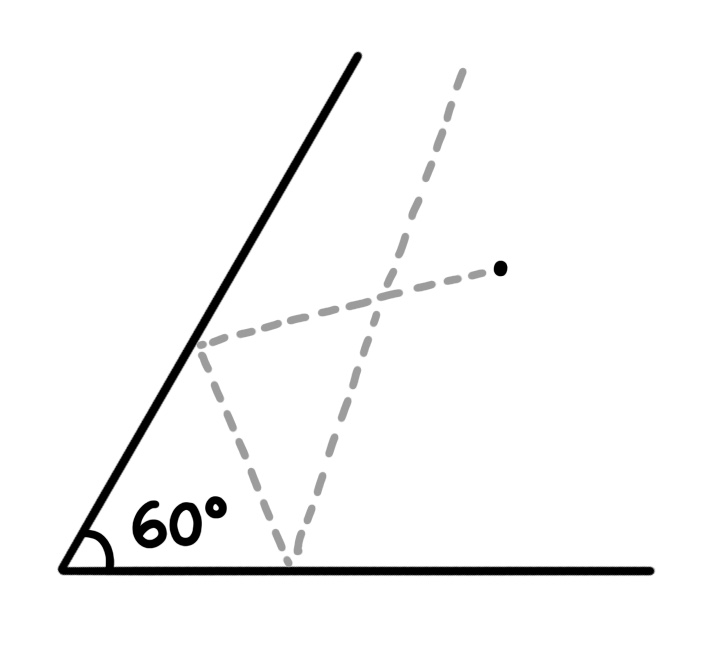

페르마의 원리에 따라, 빛은 반사될 때 최소시간이 걸리는 경로 (= 직선) 를 택한다.

빛의 입사각과 반사각이 같다는 성질을 이용해서, 두 개의 거울을 특정 각도로 놓았을 때 원하는 모양을 나타낼 수 있을지 궁금했다.

Untitled_Artwork_3.jpg

중력이 수평면에 평행하게 작용한다고 가정하면 사이클로이드는 최단거리가 된다. 하지만 실제로는 지구는 구형이다. 구형에 작용하는 중력 즉, 보다 넓게 보았을때 최소 경로는 어떤 모양이 나올까?

'지구는 둥글다'라는 현대에서 보면 아주 기초적인 사실을 바탕으로 궁금증이 생겼다.

어떤 직선 위에 원이 놓여있다. 그리고 이 원의 원주에 한 점을 찍고 굴린 자취를 그린 사이클로이드를 그린다. 이때 이 사이클로이드 곡선의 밑넓이와 원의 넓이 사이의 관계를 설명하여라.

일반적인 함수식을 가진 곡선의 밑면적을 구하는 것은 쉽게 가능하지만 사이클로이드의 밑 면적을 구하는 방법은 쉽게 떠오르지 않아 한번 고민해보고 싶었다.

5X5칸이 있다. 이 칸을 직선으로 움직일때 양 끝에서 끝 점까지 직선으로 가는 최단거리의 수를 구하여라

서울같은 곳은 길이 바둑판 모양이라고 해서 가장 빠르게 가는 길이 궁금했기 때문이다.

사이클로이드 선 위로 원을 굴렸을 때 원주 위의 한 정점이 그리는 곡선인데 이 곡선을 활용해 물체가 내려올 때 가장 빠르다고 한다. 그렇다면 과연 사이클로이드 곡선에서 어떤 모양의 물체를 내려보내야 가장 빠른 시간에 도착할까?(사이클로이드 곡선에서 마찰력이 있을 때 없을 때 둘 다 생각, 공기저항 무시) 또한, 사이클로이드 곡선과 유사하게 사이클로이드 곡선은 원을 이용했지만 다른 도형을 활용한 곡선은 어떤 모양이 나오고 위 도형을 활용한 것의 최단시간일까?

사이클로이드 곡선에서 내려보내는 모양은 항상 원 밖에 보지 못 해서 다른 삼각형이나 사각형을 굴리면 어떻게 될 지 궁금해졌기 때문이다.

보통 최단 경로하면 하나의 물체의 최단경로를 이야기 하지만 하나가 아닌 n개의 물체에 대해 효율적으로 움직여서 어느 지점으로 최단거리로 가는 방법이 궁금합니다. 또 2차원이 아닌 3차원 공간에서,  여러가지 제한 요소가 들어 있을때 어떻게 하면 효율적으로 이동할수 있는가가 궁금하고 이런 내용이 실생활에서 택시, 경찰차, 소방차 등 어떤 장소로 빠르게 가야되는 직업에서 이런 내용이 적용이 되는지 궁금합니다.

코딩 문제를 풀면서 2개의 경찰차를 움직여 최소의 이동으로 원하는 지점을 도달하는 문제가 있는데 이런 문제를 풀면서 공간이 2차원이 아닌 3차원에서, 이동에 제한이 있고 2개가 아닌 n개를 가지고 할때 어떻게 할 수 있을지 궁금하게 되었고 또 경찰차나 소방차등 효율적으로 일을 처리해야되는 사람들에게 필요할꺼 같기도 해서 질문을 올리게 되었습니다.

대한민국에 있는 많은 놀이공원에는 후룸라이드가 있다. 그런데 그중 대부분은 가장 빠른 속도를 낼 수 있는 싸이클로이드가 아닌 직선을 택하고 있다. 이유가 무엇일까?

후룸라이드가 타 롤러코스터 대비 너무 재미가 없어서 하게 되었다.

3차원 택시기하학으로 구를 만들면 어떤 모야미 나올까?

2차원일태 원이 택시기하학에서 다르다고 해서

1초에 1씩 이동하는 A(0,-2)가 B(0,2)로 가려고 한다.이때 중심이(0,0)이며 반지름이 1인 원에 닿으면 1초에 0.5씩 움직이게 된다. 이때 걸린 시간을 x, 이동 거리를 y라 할때 x+y가 최솟값과 그때의 경로를 구하시오.

최단거리만 고려하는 것이 아닌 이동 시간까지 생각하는 것이 주변에 더 많이 사용되는 것 같아서 이 문제를 만들었다.

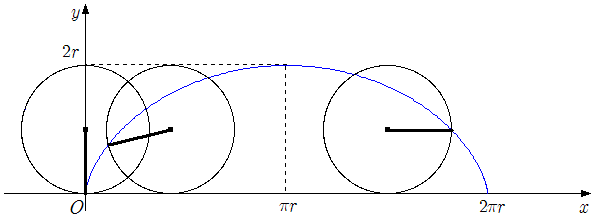
강에 다리 (XY) 를 놓으려고 한다. 이때, AX + XY + YB 가 최소가 되는 X의 위치는 어디일까?

(이때, 직선 m과 직선 n은 평행하다.)

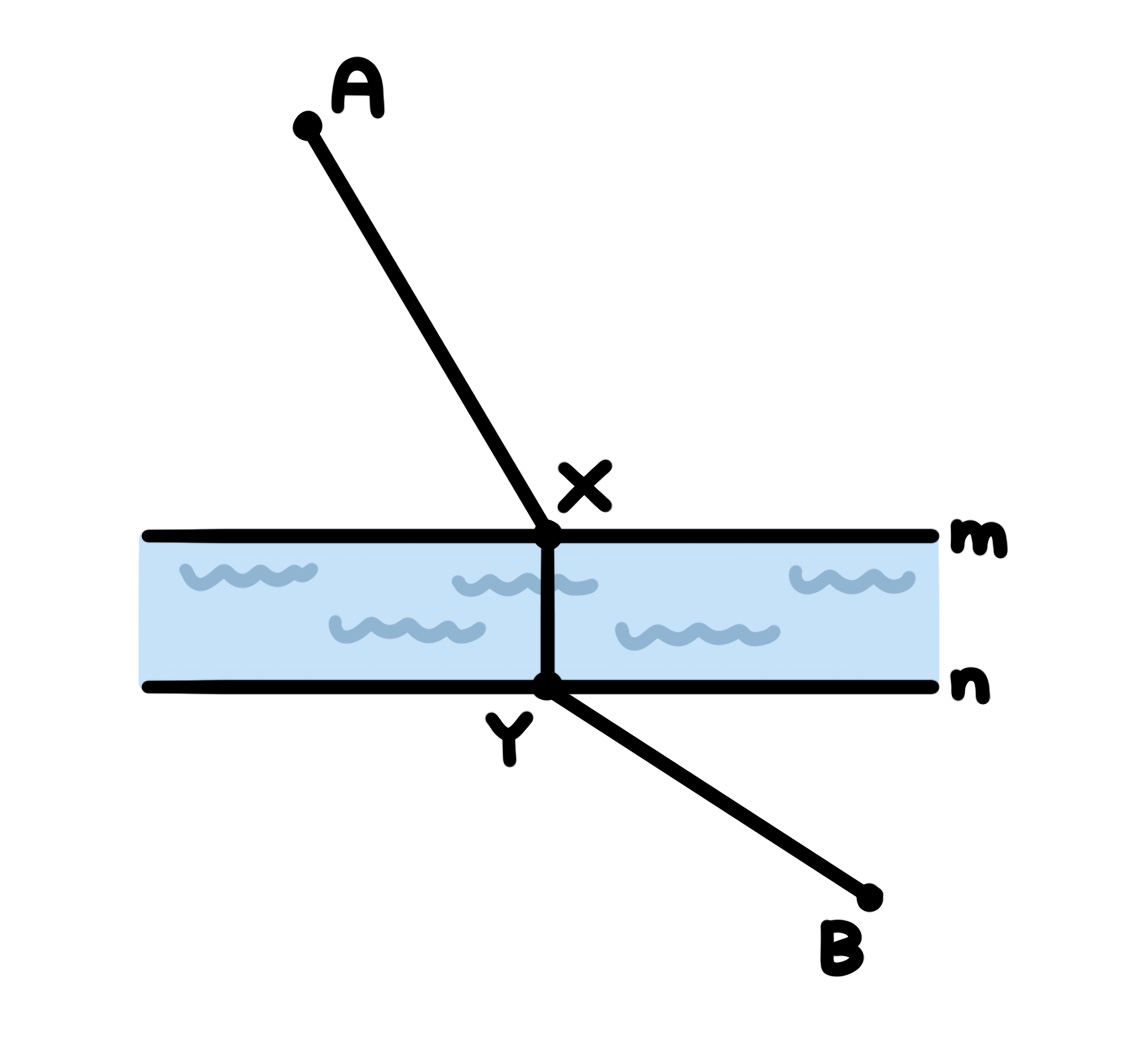
한 점에서 다른 점으로 가는 최단 거리를 구할 때, 강을 건너는 다리가 필요할 경우에는 어떻게 계산해야 할지 궁금했다.

Untitled_Artwork_2.jpg

아래와 같이 좌표평면 위의  두점과 X축위를 움직이는 점 P가 있다. 이때, 선분 AP+선분AB의 길이가 가장 짧았을 때의 P의 위치의 평면거울을 B점을 바라보게 놓는다. 이때, B와 B의 상까지의 거리를 구하여라

문제집의 문제를 풀다가 너무 재미있어서 약간 변형해 보았다

두 점을 곡선으로 연결할 때 최대 거리는 얼마인가요?

최단 거리는 두 점을 잇는 직선이라 측정이 가능하다고 배웠는 데 최대 거리는 알려주지 않아서 궁금했었다

선분을 사용해 사이클로이드 곡선과 비슷한 모양으로 이동을 하면 둘 중 무엇이 더 빠를까?

선분으로 사이클로이드 곡선과 비슷한 모양을 만들어 이동하면 거리는 더 줄고 사이클로이드 곡선과 비슷한 모양인데 더 빨라질 수도 있지 않을까 궁금증이 생겼다.

바다속 심해에서 예를 들어 우리나라 바닷속에서 잠수함을 타고 우리나라의 반대편인 아르헨티나까지 최단 경로로 가는 방법

비행기가 하늘에서 곡선으로 최단 거리로 가는
것 처럼 잠수함도 비행기 처럼 최단 거리로
가는 방법이 궁금해서.

곡선 k와 직선 y가 한 점에서 만난다. 이때곡선 원 O는 곡선 k와 직선 y와 모두 접하여 있다. 
곡선 k의 식이 y = 3x^2-4x+11이다. 원 O의 크기가 최대가 되도록 하는 직선 y의 식을 구하시오.

이차함수 단원을 공부하고 직선과 원에 관심을 가지고 수학 공부를 하다 보니 곡선, 직선, 원 모두 한 문제 속에 등장하면 어떨까하는 생각을 하게 되었고 문제를 만들어보았다.

새가 먹잇감을 잡기위해 착륙하는 과정에서 사이클로이드 곡선형으로 착륙한다. 만약 새가 직선으로 착륙한다면 사이클로이드 곡선형으로 착륙할 때와 속도적인 측면에서 어느 정도 차이가 날까? 먹잇감을 놓칠만큼 차이가 날까?

새의 착륙 과정에서 사이클로이드 곡선형의 착륙과 직선형의 착륙은 어느 정도 속도 차이가 날지 궁금했다.

학교 사회 시간에 다양한 나라의 가옥과 이의 특징에 대해 조사했다.
가장 인상 깊었던 것은 일본은 눈이 많이 내려서 전통 가옥의 지붕이 뾰족하다는 점이었다.
(사진에서 알 수 있듯이) 일본의 지붕은 지선이다.만약 이를 사이클로이드 곡선의 형태로 바꾸면 눈이 더 빠르게 흘러내려 가장 효율적인  형태의 지붕이 될 수 있었을까?

사회 시간에 조사했던 가옥의 특징 중 일본은 눈이 쌓이지 않게 지붕이 가파랐다(빨리 흘러내리게 하기 위해서).
지붕의 꼭대기에서 사이클로이드 곡선과 그냥 직선 중 더 효율적으로눈을 흘러내리게 할 수 있는 구조는 무엇일까 궁금해졌다.

문제: 그림

A에서 B로 가는 최단거리를 구해라!! 최대한 효율적이게!!




1. 빨간색 상관없이 가는데 최단 거리는 몇가지 인가요?
1x1이 직선이라고 생각하세요!! 

예)



2. 만약 대각선도 되면 가장 짧은 길이는 어떻게 될까요?
이거는 그냥선(1x1아님)

만약 같은 경우가 여러가지라면 몇개인가요??


예)


1,2번 건물 못 뚫음!!

3. 한칸을 가는데 1분이 걸리고 빨간색을 밟았을때 3분이 더 소요된다면 무슨길이 가장 효율적일까요? 길이는 짧게 시간도 짧게!
1번과 같이 1x1이 한 직선!

학교를 가는데 어떤 길을 가는게 효율적인지 궁금해서입니다( 참고로 빨간색은 신호등 역할)

wLS.png
ㅡㄱ냥.png
depositphotos_43717425-stock-illustration-graph-paper-pattern-real-scale.png

사이클로이드는, 최대한 짧은 시간에 내려가는 곡선이다. 모든 것이 직선인 택시기하학에서의  사이클로이드는 무었일까?

택시기하학에서는 원, 타원, 포물선 등이 우리가 아는것과 다 달라서.

지구에서 이동 방법은 크게 3개가 있다. 육지, 바다, 그리고 하늘인데, 육지가 가장 간단하지만 무조건 일직선으로 가는 것이 불가능하다는 단점이 있다. 바다는 해류를 감안해야 하고, 하늘은 직선 이동은 쉬우나 대지나 바다보다 이동이 어려운 점이 있다. 이때, 이동이 가장 용이한 부분은 어디일까?

최단거리라고 할 때, 우리는 보통 GPS상의 육료를 많이 보아서 이런 질문을 생각하게 되었다. 

유클리드공간상에서의 최단거리(두 점 사이의 거리 중 가장 짧은 크기를 갖는 것)란 직선을 의미하지만 비유클리드공간에서의 최단거리란 주어진 공간상의 관통이 공간상의 직선보다 최단거리가 될 수 있다.
우리는 3차원 공간상에 존재하기에 그 위의 여분차원이 실존하는지에 관해 알수 있는방법이 거의없지만 만약 공간상의 관통 즉 웜홀이 실존한다면 또 다시 웜홀을 통한 공간이동이 관통할 수 있는최소한의 거리인지에 관해 의문을 가질 수 밖에 없는 것일까? 쉽게 말하면 더 상위차원의 존재가 증명될 경우 더 높은 상위차원으로 갈 수록 최단거리에 가까워진다고 볼수 있는가?

 

추가설명

학자에 따라 다소 차이가 있지만) 적어도 10~12개의 차원들로 이뤄져 있다고 한다. 3차원 이상 되는 여분의 차원들이 맨눈에 보이지 않는 것은 그것들이 아주 작게 돌돌 말려 있거나(칼라비-야우 다양체), 우리 우주가 11차원 시공 내의 4차원 막에 있기(랜들-선드럼 모형) 때문이다.

우리 우주가 실제로 몇 차원으로 되어있느냐는 문제와는 별개로, 적어도 한 가지 분명한 것은 4차원 시공간 이상의 상위차원에서는 입체적인 물질이 형성될 수 있다는 사실이다. 그렇다면 6차원이나 9차원의 환경에서도 체액을 온전히 담고 있는 단단한 몸을 지닌 생명이 살고 있을지 모른다.

사이클로이드 곡선과 직선은 어느 정도의 거리 차이가 날까?
좌표평면 위에서 (5,5)와 같은 좌표가 주어졌을 때, 한 칸(x축, y축 unit 1씩의 칸)당 속도를 1초라고 할 때, 사이클로이드와 직선의 원점까지의 도착 경로에서 얼마만큼의 시간은 차이가 날까?

항상 사이클로이드 곡선이 직선보다 빠른 곡선이라고 하는데 얼마나 빠를지 궁금하였다. 시간으로 확실하게 어떻게 빠른지 계산할 수 있을지 의문이 생겼다.

한 변의 길이가 1인 정사각형 ABCD가 있다
한꼭짓점 A에서 반대쪽 꼭짓점 C까지 변을 통해 가게 되면
변 AB와 변 BC를 지나 갈 것이다. 변 두개를 지났으니 거리는 2이다.
그러나 변 AB와 BC 의 중심에 중점 Q,P를 그려 보자. 그리고 Q,P에서 각각 수선을 그어 그것들의 교점을 T라 해 보자.
그러면 우리는 AQ, QT, TP, PC 순서로 이동할 수 있으며, 여전히 거리는 2일 것이다.
이러한 과정을 계속 반복한다면 꺽인 선들은 결국엔 극한의 개념과 같이 '직선'의 형태를 띄게 될 것이다.

그런데,,... 이렇게 만들어진 직선은 결국 대각선이 아닌가?
그리고, 정사각형의 대각선 공식을 통해 대각선이 루트2 라는 것을 알 수 있는데
그렇다면 루트2는 2라는 식이 나올 수 있지 않을까?
 

극한과 도형을 배우다가 딴생각을 하게 되었는데 그 때 문뜩 든 생각.

우리나라의 한옥의 경우 지붕의 모양이 직선이 아니라 약간 휘어진 곡선으로 되어 있다. 그러나 서양식 건물의 지붕은 보통 직선으로 되어 있다. 동서양 건축물의 지붕이 차이가 나는 이유는 뭘까?  

동 서양 지역의 자연환경은 서로 비슷한 점이 많은데 동양 견축물의 지붕이 더 곡선인 것 같다 궁금증이 들었다. 

문제: 다음 그림에서 A 부터 B 까지 갈 수 있는 최단경로는 얼마이며, 그 경우의 수는 몇가지인지 구하시오. ( 단, 이동할 때에는 곡선을 따라 움직이며, 점 단위로 한칸씩 갈 수 있다.)
* 예시 답: 3개의 점, 5가지

보통 최단경로 문제는 직선 경로가 대다수이다. 그래서 곡선이 포함되어 조금 더 생각이 필요한 문제를 만들고 싶었다.

제목_없음.png

똑똑한 인공지능과 엉뚱한 초등학생이 말싸움을 하게 되면
누가 이기게 될까?

초등학생끼리 말싸움을 하면 결과를 예측하기가 쉽다. 당연히 말빨이 좋으면 이긴다.
하지만 똑똑하고 고지식한 인공지능과 초등학생이 싸우다면 엉뚱한 일이 벌어지거나 
인공지능, 또는 초등학생 둘중 한명만이 당황하게 되는 상황이 일어날 것이다.
그래서 궁금해졌다.

미끄럼틀을 탄다고 생각해 보자. 수학적으로는 사이클로이드가 최단거리이다. 하지만 현실에서는 중력 같은 다양한 원인으로 인해 다른 결과가 나올 수 있다. 그렇다면 이러한 점을 고려해서 중력의 크기나 미끄럼틀의 재질, 탑승자의 무게 등으로 걸리는 시간을 바꿀 수 있을 것이다. 이러한 것으로는 어떤 것이 있을까? 이렇게 되면 최단'거리'라고 할 수는 없는 것일까?

직선으로 갈 때 곡선보다 더 빠르게 갈 수 있는 방법은 뭐가 있을까 궁금해졌다. 

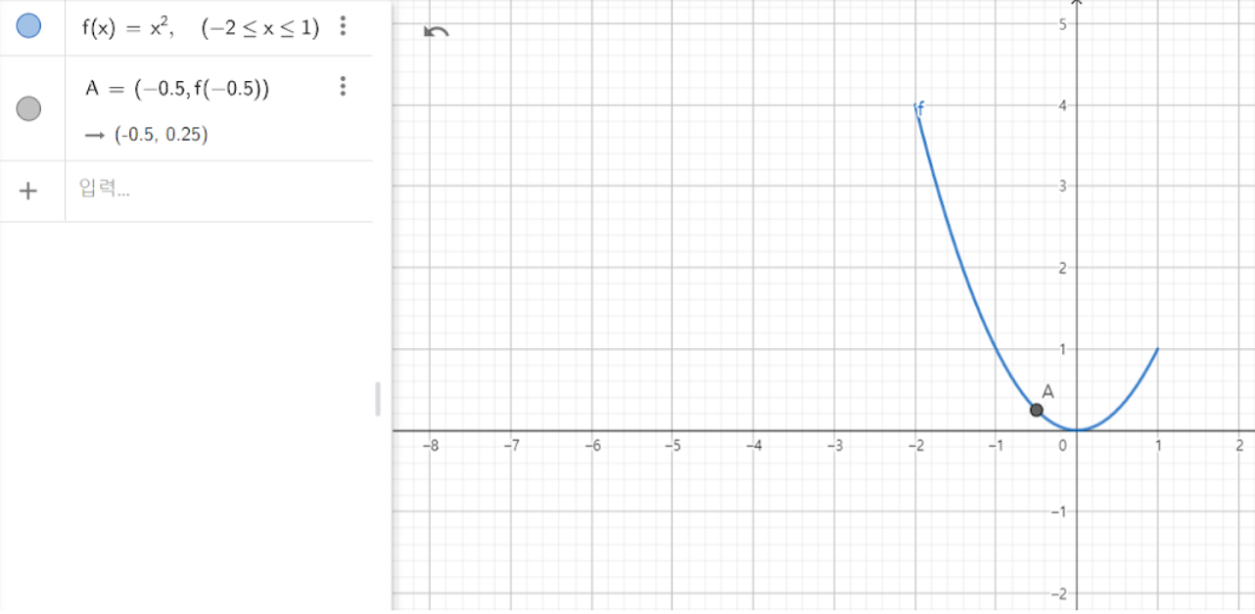
어느 건물 옥상에서 똑바로 위로 던져 올린 물체의 t초 후의 높이 hm가 h =- 4.9(t제곱-4t-12)일 때, 다음을 구해보자

1. 물체가 최고 높이에 도달하는 시각
2. 물체가 지면에 도달하는 순간의 속도

 속력은 단순한 빠르기를 의미하며, 단위 시간당 이동 거리로 측정한다. 반면에 속도는 속력에 방향이 더해진 것이다. 속력은 이동 경로및 방향을 갖지 않고 거리를 시간으로 나누는 값으로 표현된다.
공을 던져 올리고 그 공이 떨어지면 포물선(곡선)을 그리고, 속도와 속력의 차이가 방향(이동경로)를 고려하느냐 마느냐에서 발생하기 때문에 이런 문제를 생각해보았다.

알버트 아인슈타인이 발표한 "일반상대성이론"에는 "중력이 시공간을 구부려서 빛이 구부러지고 시간이 느려진다"라고 했다. 그 말은 즉 빛이 직선으로 갈 때가 곡선 모양으로 갈 때보다 더 빠르게 목적지에 도달할 수 있다는 얘기다. 그런데 만일 빛이 구부러질 때 우연히 사이클로이드 곡선 모양으로 구부러진다면, 오히려 시간은 더 빨리 가게 될까?

영재원 수업을 듣다가 일반상대성이론과 관련있는 개념이 나왔는데, 그것을 보고 궁금해졌다.

만약 행성이 구가 아니라면 사이클로이드가 아닌 경로가 최단거리가 될까요?

지구는 사실상 구인 상황인데 구가 아니고 정 12각형같은 애매한 모양의 행성이라면 중력의 방향이 달라져서 다른 경로가 최소가 될 수도 있을거 같아서 질문해 보았습니다.

경복궁의 처마와 연잎의 잎도 사이클로이드 곡선일까?

경복궁을 갔을 때 그곳에서 처마가 곡선인 것과 연잎이 곡선인 것을 보았다. 그래서 혹시 그 곳선들이 모두 사이클로이드 곡선일 지 궁금했다.그리고 만일 아니라도 사이클로이드 곡선을  실생활에 접목할 수 있을 것 같다는 생각이 들어서.

어떤 조건이 있으면 직선이 사이클로이드 곡선보다 빠를 수 있을까?

직선이 선중에 가장 빠르다고 생각 하던 사람들이 있기 때문에

평면에서의 최단 거리는 직선이다. 그렇다면 구(지구)의 표면에서의 최단거리는 직선일까 곡선일까? 또한, 더 빨리 낙하 하기 위해서는 어떤 자세로 해야할까?

하늘에서의 최단거리와 어떻게 더 빨리 낙하 할 수 있을지 궁금하다.

직선과 곡선중 공기저항을 뭐가 더 많이받을까?

공기저항이 크면 속도사 줄어드니까

다음 그림은 한 변의 길이가 1인 정육각형을 벌집모양으로 붙여 만든 것이다. 이떄, A지점에서 출발하여 변을 따라 움직여서 최단거리로 B지점까지 이동하는 방법의 수를 구하여라.

벌집과 관련된 최단경로 문제를 만들고 싶었다.

단위 격자점 4X4가 있다. 적당한 격자점 하나를 출발점으로 하고 그 다음부터 두 격자점 사이의 거리가 점점 멀어지게 격자점들을 선택해 나가자. 단 한 번 선택했던 격자점을 또 선택하면 안 된다. 이런 식으로 선택할 수 있는 최대 격자점의 수를 a라 하고, a개의 격자점을 선택하는 경로의 수를 b라고 할때, ab의 값을 구하여라.

피타고라스 정리와 관련된 경로 문제를 만들고 싶었다.

직접 문제를 만들어보고 싶었다. 특히 첫번째 문제는 유치해보일 수도 있지만 재밌게 만드려고 노력해봤다.